AerStatevector#

class AerStatevector(data, dims=None, **configs)[source]#

Bases: Statevector

AerStatevector class

This class inherits Statevector, which stores probability amplitudes in its ndarray. class:AerStatevector generates this ndarray by using the same runtime with AerSimulator.

Parameters:

or (data (np.array or list or Statevector or AerStatevector or QuantumCircuit) – qiskit.circuit.Instruction): Data from which the statevector can be constructed. This can be either a complex vector, another statevector or a QuantumCircuit or Instruction (Operator is not supported in the current implementation). If the data is a circuit or instruction, the statevector is constructed by assuming that all qubits are initialized to the zero state.
dims (int or tuple or list) – Optional. The subsystem dimension of the state (See additional information).
configs (kwargs) – configurations of AerSimulator. method configuration must be statevector or matrix_product_state.

Raises:

AerError – if input data is not valid.

Additional Information:: The dims kwarg is used to Statevector constructor.

Attributes

atol = 1e-08#

data#: Return data.

dim#: Return total state dimension.

num_qubits#: Return the number of qubits if a N-qubit state or None otherwise.

rtol = 1e-05#

settings#: Return settings.

Methods

__getitem__(key: int | str) → np.complex128[source]#

Return Statevector item either by index or binary label :param key: index or corresponding binary label, e.g. ‘01’ = 1. :type key: int or str

Returns:: Statevector item.
Return type:: numpy.complex128
Raises:: QiskitError – if key is not valid.

__len__()[source]#

__mul__(other)[source]#

conjugate()[source]#: Return the conjugate of the operator.

copy()[source]#: Make a copy of current operator.

dims(qargs=None)[source]#: Return tuple of input dimension for specified subsystems.

draw(output: str | None = None, **drawer_args)[source]#

Return a visualization of the Statevector.

repr: ASCII TextMatrix of the state’s __repr__.

text: ASCII TextMatrix that can be printed in the console.

latex: An IPython Latex object for displaying in Jupyter Notebooks.

latex_source: Raw, uncompiled ASCII source to generate array using LaTeX.

qsphere: Matplotlib figure, rendering of statevector using plot_state_qsphere().

hinton: Matplotlib figure, rendering of statevector using plot_state_hinton().

bloch: Matplotlib figure, rendering of statevector using plot_bloch_multivector().

city: Matplotlib figure, rendering of statevector using plot_state_city().

paulivec: Matplotlib figure, rendering of statevector using plot_state_paulivec().

Parameters:

output (str) – Select the output method to use for drawing the state. Valid choices are repr, text, latex, latex_source, qsphere, hinton, bloch, city, or paulivec. Default is repr. Default can be changed by adding the line state_drawer = <default> to ~/.qiskit/settings.conf under [default].
drawer_args – Arguments to be passed directly to the relevant drawing function or constructor (TextMatrix(), array_to_latex(), plot_state_qsphere(), plot_state_hinton() or plot_bloch_multivector()). See the relevant function under qiskit.visualization for that function’s documentation.

Returns:

matplotlib.Figure or str or TextMatrix or IPython.display.Latex: Drawing of the Statevector.

Raises:

ValueError – when an invalid output method is selected.

Examples

Plot one of the Bell states

from numpy import sqrt
from qiskit.quantum_info import Statevector
sv=Statevector([1/sqrt(2), 0, 0, -1/sqrt(2)])
sv.draw(output='hinton')

(Source code, png, hires.png, pdf)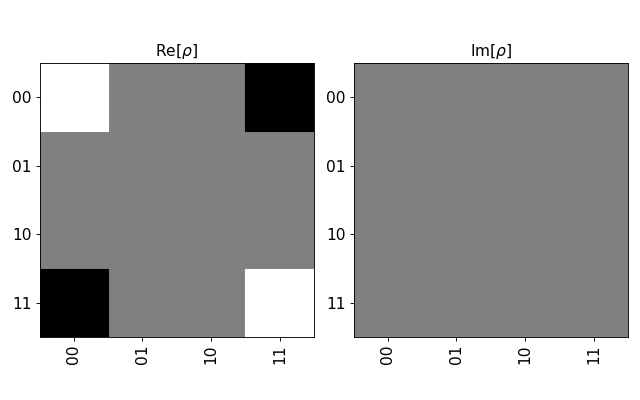

../_images/qiskit_aer-quantum_info-AerStatevector-1.png

equiv(other: Statevector, rtol: float | None = None, atol: float | None = None) → bool[source]#

Return True if other is equivalent as a statevector up to global phase.

Note

If other is not a Statevector, but can be used to initialize a statevector object, this will check that Statevector(other) is equivalent to the current statevector up to global phase.

Parameters:

other (Statevector) – an object from which a Statevector can be constructed.
rtol (float) – relative tolerance value for comparison.
atol (float) – absolute tolerance value for comparison.

Returns:

True if statevectors are equivalent up to global phase.

Return type:

bool

evolve(other: Operator | QuantumCircuit | Instruction, qargs: list[int] | None = None) → Statevector[source]#

Evolve a quantum state by the operator.

Parameters:

other (Operator | QuantumCircuit | circuit.Instruction) – The operator to evolve by.
qargs (list) – a list of Statevector subsystem positions to apply the operator on.

Returns:

the output quantum state.

Return type:

Statevector

Raises:

QiskitError – if the operator dimension does not match the specified Statevector subsystem dimensions.

expand(other: Statevector) → Statevector[source]#

Return the tensor product state other ⊗ self.

Parameters:: other (Statevector) – a quantum state object.
Returns:: the tensor product state other ⊗ self.
Return type:: Statevector
Raises:: QiskitError – if other is not a quantum state.

expectation_value(oper: BaseOperator | QuantumCircuit | Instruction, qargs: None | list[int] = None) → complex[source]#

Compute the expectation value of an operator.

Parameters:

oper (Operator) – an operator to evaluate expval of.
qargs (None or list) – subsystems to apply operator on.

Returns:

the expectation value.

Return type:

complex

classmethod from_instruction(instruction)[source]#

Return the output statevector of an instruction.

The statevector is initialized in the state \(|{0,\ldots,0}\rangle\) of the same number of qubits as the input instruction or circuit, evolved by the input instruction, and the output statevector returned.

Parameters:: instruction (qiskit.circuit.Instruction or QuantumCircuit) – instruction or circuit
Returns:: The final statevector.
Return type:: Statevector
Raises:: QiskitError – if the instruction contains invalid instructions for the statevector simulation.

static from_int(i, dims)[source]#

Return a computational basis statevector.

Parameters:

i (int) – the basis state element.
dims (int or tuple or list) – The subsystem dimensions of the statevector (See additional information).

Returns:

The computational basis state \(|i\rangle\).

Return type:

Statevector

Additional Information:

The dims kwarg can be an integer or an iterable of integers.

Iterable – the subsystem dimensions are the values in the list with the total number of subsystems given by the length of the list.
Int – the integer specifies the total dimension of the state. If it is a power of two the state will be initialized as an N-qubit state. If it is not a power of two the state will have a single d-dimensional subsystem.

classmethod from_label(label)[source]#

Return a tensor product of Pauli X,Y,Z eigenstates.

Table 1 Single-qubit state labels#
Label	Statevector
`"0"`	\([1, 0]\)
`"1"`	\([0, 1]\)
`"+"`	\([1 / \sqrt{2}, 1 / \sqrt{2}]\)
`"-"`	\([1 / \sqrt{2}, -1 / \sqrt{2}]\)
`"r"`	\([1 / \sqrt{2}, i / \sqrt{2}]\)
`"l"`	\([1 / \sqrt{2}, -i / \sqrt{2}]\)

Parameters:: label (string) – a eigenstate string ket label (see table for allowed values).
Returns:: The N-qubit basis state density matrix.
Return type:: Statevector
Raises:: QiskitError – if the label contains invalid characters, or the length of the label is larger than an explicitly specified num_qubits.

inner(other: Statevector) → complex128[source]#

Return the inner product of self and other as \(\langle self| other \rangle\).

Parameters:: other (Statevector) – a quantum state object.
Returns:: the inner product of self and other, \(\langle self| other \rangle\).
Return type:: np.complex128
Raises:: QiskitError – if other is not a quantum state or has different dimension.

is_valid(atol: float | None = None, rtol: float | None = None) → bool[source]#: Return True if a Statevector has norm 1.

measure(qargs: list | None = None) → tuple[source]#

Measure subsystems and return outcome and post-measure state.

Note that this function uses the QuantumStates internal random number generator for sampling the measurement outcome. The RNG seed can be set using the seed() method.

Parameters:

qargs (list or None) – subsystems to sample measurements for, if None sample measurement of all subsystems (Default: None).

Returns:

the pair (outcome, state) where outcome is the: measurement outcome string label, and state is the collapsed post-measurement state for the corresponding outcome.

Return type:

tuple

metadata()[source]#: Return result metadata of an operation that executed lastly.

probabilities(qargs: None | list[int] = None, decimals: None | int = None) → np.ndarray[source]#

Return the subsystem measurement probability vector.

Measurement probabilities are with respect to measurement in the computation (diagonal) basis.

Parameters:

qargs (None or list) – subsystems to return probabilities for, if None return for all subsystems (Default: None).
decimals (None or int) – the number of decimal places to round values. If None no rounding is done (Default: None).

Returns:

The Numpy vector array of probabilities.

Return type:

np.array

Examples

Consider a 2-qubit product state \(|\psi\rangle=|+\rangle\otimes|0\rangle\).

from qiskit.quantum_info import Statevector

psi = Statevector.from_label('+0')

# Probabilities for measuring both qubits
probs = psi.probabilities()
print('probs: {}'.format(probs))

# Probabilities for measuring only qubit-0
probs_qubit_0 = psi.probabilities([0])
print('Qubit-0 probs: {}'.format(probs_qubit_0))

# Probabilities for measuring only qubit-1
probs_qubit_1 = psi.probabilities([1])
print('Qubit-1 probs: {}'.format(probs_qubit_1))

probs: [0.5 0.  0.5 0. ]
Qubit-0 probs: [1. 0.]
Qubit-1 probs: [0.5 0.5]

We can also permute the order of qubits in the qargs list to change the qubit position in the probabilities output

from qiskit.quantum_info import Statevector

psi = Statevector.from_label('+0')

# Probabilities for measuring both qubits
probs = psi.probabilities([0, 1])
print('probs: {}'.format(probs))

# Probabilities for measuring both qubits
# but swapping qubits 0 and 1 in output
probs_swapped = psi.probabilities([1, 0])
print('Swapped probs: {}'.format(probs_swapped))

probs: [0.5 0.  0.5 0. ]
Swapped probs: [0.5 0.5 0.  0. ]

probabilities_dict(qargs: None | list = None, decimals: None | int = None) → dict[source]#

Return the subsystem measurement probability dictionary.

Measurement probabilities are with respect to measurement in the computation (diagonal) basis.

This dictionary representation uses a Ket-like notation where the dictionary keys are qudit strings for the subsystem basis vectors. If any subsystem has a dimension greater than 10 comma delimiters are inserted between integers so that subsystems can be distinguished.

Parameters:

qargs (None or list) – subsystems to return probabilities for, if None return for all subsystems (Default: None).
decimals (None or int) – the number of decimal places to round values. If None no rounding is done (Default: None).

Returns:

The measurement probabilities in dict (ket) form.

Return type:

dict

purity() → float64[source]#: Return the purity of the quantum state.

reset(qargs: list[int] | None = None) → Statevector[source]#

Reset state or subsystems to the 0-state.

Parameters:: qargs (list or None) – subsystems to reset, if None all subsystems will be reset to their 0-state (Default: None).
Returns:: the reset state.
Return type:: Statevector

Additional Information:: If all subsystems are reset this will return the ground state on all subsystems. If only a some subsystems are reset this function will perform a measurement on those subsystems and evolve the subsystems so that the collapsed post-measurement states are rotated to the 0-state. The RNG seed for this sampling can be set using the seed() method.

reverse_qargs() → Statevector[source]#

Return a Statevector with reversed subsystem ordering.

For a tensor product state this is equivalent to reversing the order of tensor product subsystems. For a statevector \(|\psi \rangle = |\psi_{n-1} \rangle \otimes ... \otimes |\psi_0 \rangle\) the returned statevector will be \(|\psi_{0} \rangle \otimes ... \otimes |\psi_{n-1} \rangle\).

Returns:: the Statevector with reversed subsystem order.
Return type:: Statevector

sample_counts(shots: int, qargs: None | list = None) → Counts[source]#

Sample a dict of qubit measurement outcomes in the computational basis.

Parameters:

shots (int) – number of samples to generate.
qargs (None or list) – subsystems to sample measurements for, if None sample measurement of all subsystems (Default: None).

Returns:

sampled counts dictionary.

Return type:

Counts

Additional Information:

This function samples measurement outcomes using the measure probabilities() for the current state and qargs. It does not actually implement the measurement so the current state is not modified.

The seed for random number generator used for sampling can be set to a fixed value by using the stats seed() method.

sample_memory(shots, qargs=None)[source]#

Sample a list of qubit measurement outcomes in the computational basis.

Parameters:

shots (int) – number of samples to generate.
qargs (None or list) – subsystems to sample measurements for, if None sample measurement of all subsystems (Default: None).

Returns:

list of sampled counts if the order sampled.

Return type:

np.array

Additional Information:

This function samples measurement outcomes using the measure probabilities() for the current state and qargs. It does not actually implement the measurement so the current state is not modified.

The seed for random number generator used for sampling can be set to a fixed value by using the stats seed() method.

seed(value=None)[source]#: Set the seed for the quantum state RNG.

tensor(other: Statevector) → Statevector[source]#

Return the tensor product state self ⊗ other.

Parameters:: other (Statevector) – a quantum state object.
Returns:: the tensor product operator self ⊗ other.
Return type:: Statevector
Raises:: QiskitError – if other is not a quantum state.

to_dict(decimals: None | int = None) → dict[source]#

Convert the statevector to dictionary form.

Parameters:: decimals (None or int) – the number of decimal places to round values. If None no rounding is done (Default: None).
Returns:: the dictionary form of the Statevector.
Return type:: dict

Example

The ket-form of a 2-qubit statevector \(|\psi\rangle = |-\rangle\otimes |0\rangle\)

from qiskit.quantum_info import Statevector

psi = Statevector.from_label('-0')
print(psi.to_dict())

{'00': (0.7071067811865475+0j), '10': (-0.7071067811865475+0j)}

For non-qubit subsystems the integer range can go from 0 to 9. For example in a qutrit system

import numpy as np
from qiskit.quantum_info import Statevector

vec = np.zeros(9)
vec[0] = 1 / np.sqrt(2)
vec[-1] = 1 / np.sqrt(2)
psi = Statevector(vec, dims=(3, 3))
print(psi.to_dict())

{'00': (0.7071067811865475+0j), '22': (0.7071067811865475+0j)}

For large subsystem dimensions delimiters are required. The following example is for a 20-dimensional system consisting of a qubit and 10-dimensional qudit.

import numpy as np
from qiskit.quantum_info import Statevector

vec = np.zeros(2 * 10)
vec[0] = 1 / np.sqrt(2)
vec[-1] = 1 / np.sqrt(2)
psi = Statevector(vec, dims=(2, 10))
print(psi.to_dict())

{'00': (0.7071067811865475+0j), '91': (0.7071067811865475+0j)}

to_operator() → Operator[source]#: Convert state to a rank-1 projector operator

trace() → float64[source]#: Return the trace of the quantum state as a density matrix.