How to perform a cutting workflow with multiple observables¶

Create a circuit to cut¶

[1]:

from qiskit.circuit.library import EfficientSU2

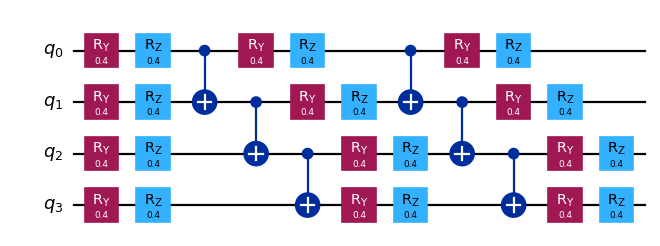
qc = EfficientSU2(4, entanglement="linear", reps=2).decompose()
qc.assign_parameters([0.4] * len(qc.parameters), inplace=True)

qc.draw("mpl", scale=0.8)

/tmp/ipykernel_3610/2689864020.py:1: DeprecationWarning: Using Qiskit with Python 3.9 is deprecated as of the 2.1.0 release. Support for running Qiskit with Python 3.9 will be removed in the 2.3.0 release, which coincides with when Python 3.9 goes end of life.
  from qiskit.circuit.library import EfficientSU2
/tmp/ipykernel_3610/2689864020.py:3: DeprecationWarning: The class ``qiskit.circuit.library.n_local.efficient_su2.EfficientSU2`` is deprecated as of Qiskit 2.1. It will be removed in Qiskit 3.0. Use the function qiskit.circuit.library.efficient_su2 instead.
  qc = EfficientSU2(4, entanglement="linear", reps=2).decompose()

[1]:

../_images/how-tos_how_to_provide_multiple_observables_2_1.png

Specify the observables of interest¶

[2]:

from qiskit.quantum_info import Pauli, SparsePauliOp

observables = [
    Pauli("-XZII"),
    SparsePauliOp(["ZZII", "IZZI", "-IIZZ", "XIXI", "ZIZZ", "IXIX"]),
]

Gather unique observable terms¶

[3]:

from qiskit_addon_cutting.utils.observable_terms import gather_unique_observable_terms

unique_observable_terms = gather_unique_observable_terms(observables)

Perform cutting workflow¶

[4]:

from qiskit_addon_cutting import partition_problem

partitioned_problem = partition_problem(
    circuit=qc, partition_labels="AABB", observables=unique_observable_terms
)
subcircuits = partitioned_problem.subcircuits
subobservables = partitioned_problem.subobservables

[5]:

import numpy as np
from qiskit_addon_cutting import generate_cutting_experiments

subexperiments, coefficients = generate_cutting_experiments(
    circuits=subcircuits, observables=subobservables, num_samples=np.inf
)

[6]:

from qiskit_ibm_runtime.fake_provider import FakeManilaV2

backend = FakeManilaV2()

/tmp/ipykernel_3610/694230361.py:1: DeprecationWarning: Using qiskit-ibm-runtime with Python 3.9 is deprecated as of the 0.41.0 release. Support for running qiskit-ibm-runtime with Python 3.9 will be removed in a future release.
  from qiskit_ibm_runtime.fake_provider import FakeManilaV2

[7]:

from qiskit.transpiler.preset_passmanagers import generate_preset_pass_manager

# Transpile the subexperiments to ISA circuits
pass_manager = generate_preset_pass_manager(optimization_level=1, backend=backend)
isa_subexperiments = {
    label: pass_manager.run(partition_subexpts)
    for label, partition_subexpts in subexperiments.items()
}

[8]:

from qiskit_ibm_runtime import SamplerV2, Batch

# Submit each partition's subexperiments as a single batch
with Batch(backend=backend) as batch:
    sampler = SamplerV2(mode=batch)
    jobs = {
        label: sampler.run(subsystem_subexpts, shots=2**12)
        for label, subsystem_subexpts in isa_subexperiments.items()
    }

[9]:

# Retrieve results
results = {label: job.result() for label, job in jobs.items()}

Reconstruct the expectation value of each unique term¶

[10]:

from qiskit_addon_cutting import reconstruct_expectation_values

# Get expectation values for each observable term
reconstructed_term_expvals = reconstruct_expectation_values(
    results,
    coefficients,
    subobservables,  # or unique_observable_terms if the circuit did not separate
)

Reconstruct the expectation value of the original operators¶

[11]:

from qiskit_addon_cutting.utils.observable_terms import (
    reconstruct_observable_expvals_from_terms,
)

reconstructed_expvals = reconstruct_observable_expvals_from_terms(
    observables, dict(zip(unique_observable_terms, reconstructed_term_expvals))
)

Compare the reconstructed expectation values with the exact expectation value from the original circuit and observables¶

[12]:

from qiskit_aer.primitives import EstimatorV2

estimator = EstimatorV2()
exact_expvals = estimator.run([(qc, observables)]).result()[0].data.evs
print(
    f"Reconstructed expectation values: {np.real(np.round(reconstructed_expvals, 8))}"
)
print(f"Exact expectation values: {np.round(exact_expvals, 8)}")
print(
    f"Error in estimation: {np.real(np.round(reconstructed_expvals-exact_expvals, 8))}"
)
print(
    f"Relative error in estimation: {np.real(np.round((reconstructed_expvals-exact_expvals) / exact_expvals, 8))}"
)

Reconstructed expectation values: [-0.15492964  0.58352631]
Exact expectation values: [-0.17994235  0.56254612]
Error in estimation: [0.02501272 0.02098019]
Relative error in estimation: [-0.13900405  0.03729506]