How to generate exact sampling coefficients

This how-to guide is intended to show users how they can generate exact sampling coefficients to be used in reconstructing the simulated expectation value of the original circuit.

First, we set up a simple cutting problem following the first tutorial.

[1]:

import numpy as np
from qiskit.circuit.library import efficient_su2
from qiskit.quantum_info import SparsePauliOp

from qiskit_addon_cutting import (
    partition_problem,
    generate_cutting_experiments,
)

/tmp/ipykernel_3514/1051240730.py:2: DeprecationWarning: Using Qiskit with Python 3.9 is deprecated as of the 2.1.0 release. Support for running Qiskit with Python 3.9 will be removed in the 2.3.0 release, which coincides with when Python 3.9 goes end of life.
  from qiskit.circuit.library import efficient_su2

[2]:

circuit = efficient_su2(4, entanglement="linear", reps=2)
circuit.assign_parameters([0.8] * len(circuit.parameters), inplace=True)
observable = SparsePauliOp(["ZZZZ"])
circuit.draw("mpl", scale=0.8)

[2]:
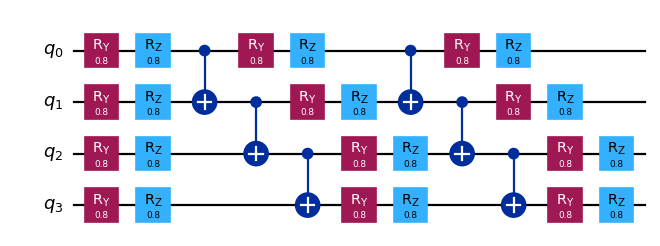
../_images/how-tos_how_to_generate_exact_sampling_coefficients_2_0.png

Partition the circuit between qubits 1 and 2 by cutting 2 CNOT gates.

[3]:

partitioned_problem = partition_problem(
    circuit=circuit, partition_labels="AABB", observables=observable.paulis
)
subcircuits = partitioned_problem.subcircuits
bases = partitioned_problem.bases
subobservables = partitioned_problem.subobservables
subcircuits["A"].draw("mpl", scale=0.6)

[3]:
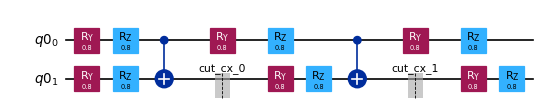
../_images/how-tos_how_to_generate_exact_sampling_coefficients_4_0.png 
[4]:

subcircuits["B"].draw("mpl", scale=0.6)

[4]:
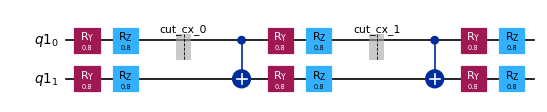
../_images/how-tos_how_to_generate_exact_sampling_coefficients_5_0.png

Demonstrate how to obtain all weights exactly

If you wish to calculate all weights exactly, no matter how small, you can achieve this by passing infinity (np.inf) to num_samples:

[5]:

subexperiments, coefficients = generate_cutting_experiments(
    circuits=subcircuits,
    observables=subobservables,
    num_samples=np.inf,
)
coefficients

[5]:

[(np.float64(0.24999999999999992), <WeightType.EXACT: 1>),
 (np.float64(0.24999999999999992), <WeightType.EXACT: 1>),
 (np.float64(0.24999999999999992), <WeightType.EXACT: 1>),
 (np.float64(-0.24999999999999992), <WeightType.EXACT: 1>),
 (np.float64(0.24999999999999992), <WeightType.EXACT: 1>),
 (np.float64(-0.24999999999999992), <WeightType.EXACT: 1>),
 (np.float64(0.24999999999999992), <WeightType.EXACT: 1>),
 (np.float64(0.24999999999999992), <WeightType.EXACT: 1>),
 (np.float64(0.24999999999999992), <WeightType.EXACT: 1>),
 (np.float64(-0.24999999999999992), <WeightType.EXACT: 1>),
 (np.float64(0.24999999999999992), <WeightType.EXACT: 1>),
 (np.float64(-0.24999999999999992), <WeightType.EXACT: 1>),
 (np.float64(0.24999999999999992), <WeightType.EXACT: 1>),
 (np.float64(0.24999999999999992), <WeightType.EXACT: 1>),
 (np.float64(0.24999999999999992), <WeightType.EXACT: 1>),
 (np.float64(-0.24999999999999992), <WeightType.EXACT: 1>),
 (np.float64(0.24999999999999992), <WeightType.EXACT: 1>),
 (np.float64(-0.24999999999999992), <WeightType.EXACT: 1>),
 (np.float64(-0.24999999999999992), <WeightType.EXACT: 1>),
 (np.float64(-0.24999999999999992), <WeightType.EXACT: 1>),
 (np.float64(-0.24999999999999992), <WeightType.EXACT: 1>),
 (np.float64(0.24999999999999992), <WeightType.EXACT: 1>),
 (np.float64(-0.24999999999999992), <WeightType.EXACT: 1>),
 (np.float64(0.24999999999999992), <WeightType.EXACT: 1>),
 (np.float64(0.24999999999999992), <WeightType.EXACT: 1>),
 (np.float64(0.24999999999999992), <WeightType.EXACT: 1>),
 (np.float64(0.24999999999999992), <WeightType.EXACT: 1>),
 (np.float64(-0.24999999999999992), <WeightType.EXACT: 1>),
 (np.float64(0.24999999999999992), <WeightType.EXACT: 1>),
 (np.float64(-0.24999999999999992), <WeightType.EXACT: 1>),
 (np.float64(-0.24999999999999992), <WeightType.EXACT: 1>),
 (np.float64(-0.24999999999999992), <WeightType.EXACT: 1>),
 (np.float64(-0.24999999999999992), <WeightType.EXACT: 1>),
 (np.float64(0.24999999999999992), <WeightType.EXACT: 1>),
 (np.float64(-0.24999999999999992), <WeightType.EXACT: 1>),
 (np.float64(0.24999999999999992), <WeightType.EXACT: 1>)]

Demonstrate how to find the minimum num_samples needed to retrieve all exact weights for 2 CNOT cuts

When num_samples is set to a finite number, each weight whose absolute value is above a threshold of 1 / num_samples will be evaluated exactly. The remaining weights – those in the tail of the distribution – will then be sampled from, resulting in at most num_samples unique weights.

In the case of a CNOT gate – or any gate equivalent to it up to single-qubit unitaries – each of the six weights of the quasi-probability decomposition have the same magnitude, so each gets sampled with a probability of \(1/6\):

[6]:

print(f"Mapping probabilities for a CNOT decomposition: {bases[0].probabilities}")

Mapping probabilities for a CNOT decomposition: [0.16666667 0.16666667 0.16666667 0.16666667 0.16666667 0.16666667]

In this example, we have cut two CNOT gates. Given that the probability of any given mapping in a CNOT decomposition is \(1/6\), the probability of any given mapping in the joint distribution combining the two cut CNOT gates is \((1/6)^2\). Therefore, we need to take at least \(6^2\) weights in order to retrieve all exact weights from generate_cutting_experiments.

[7]:

from qiskit_addon_cutting.qpd import QPDBasis
from qiskit.circuit.library.standard_gates import CXGate

qpd_basis_cx = QPDBasis.from_instruction(CXGate())


def _min_nonzero(seq, /):
    """Return the minimum value in a sequence, ignoring values near zero."""
    return min(x for x in seq if not np.isclose(x, 0))


num_cx_cuts = 2

print(
    f"Number of samples needed to retrieve exact weights: {1 / _min_nonzero(qpd_basis_cx.probabilities)**num_cx_cuts}"
)

Number of samples needed to retrieve exact weights: 36.0

Observe the coefficient weights returned from generate_cutting_experiments are WeightType.EXACT

Above, we determined 36 samples would trigger the coefficients to be returned as exact. Here we set num_samples to exactly 36 to test this.

[8]:

subexperiments, coefficients = generate_cutting_experiments(
    circuits=subcircuits,
    observables=subobservables,
    num_samples=36,
)
coefficients

[8]:

[(np.float64(0.25), <WeightType.EXACT: 1>),
 (np.float64(0.25), <WeightType.EXACT: 1>),
 (np.float64(0.25), <WeightType.EXACT: 1>),
 (np.float64(-0.25), <WeightType.EXACT: 1>),
 (np.float64(0.25), <WeightType.EXACT: 1>),
 (np.float64(-0.25), <WeightType.EXACT: 1>),
 (np.float64(0.25), <WeightType.EXACT: 1>),
 (np.float64(0.25), <WeightType.EXACT: 1>),
 (np.float64(0.25), <WeightType.EXACT: 1>),
 (np.float64(-0.25), <WeightType.EXACT: 1>),
 (np.float64(0.25), <WeightType.EXACT: 1>),
 (np.float64(-0.25), <WeightType.EXACT: 1>),
 (np.float64(0.25), <WeightType.EXACT: 1>),
 (np.float64(0.25), <WeightType.EXACT: 1>),
 (np.float64(0.25), <WeightType.EXACT: 1>),
 (np.float64(-0.25), <WeightType.EXACT: 1>),
 (np.float64(0.25), <WeightType.EXACT: 1>),
 (np.float64(-0.25), <WeightType.EXACT: 1>),
 (np.float64(-0.25), <WeightType.EXACT: 1>),
 (np.float64(-0.25), <WeightType.EXACT: 1>),
 (np.float64(-0.25), <WeightType.EXACT: 1>),
 (np.float64(0.25), <WeightType.EXACT: 1>),
 (np.float64(-0.25), <WeightType.EXACT: 1>),
 (np.float64(0.25), <WeightType.EXACT: 1>),
 (np.float64(0.25), <WeightType.EXACT: 1>),
 (np.float64(0.25), <WeightType.EXACT: 1>),
 (np.float64(0.25), <WeightType.EXACT: 1>),
 (np.float64(-0.25), <WeightType.EXACT: 1>),
 (np.float64(0.25), <WeightType.EXACT: 1>),
 (np.float64(-0.25), <WeightType.EXACT: 1>),
 (np.float64(-0.25), <WeightType.EXACT: 1>),
 (np.float64(-0.25), <WeightType.EXACT: 1>),
 (np.float64(-0.25), <WeightType.EXACT: 1>),
 (np.float64(0.25), <WeightType.EXACT: 1>),
 (np.float64(-0.25), <WeightType.EXACT: 1>),
 (np.float64(0.25), <WeightType.EXACT: 1>)]