problem_generators (qiskit_addon_utils.problem_generators)

Utility methods for problem generation.

generate_xyz_hamiltonian(coupling, *, coupling_constants=(1.0, 1.0, 1.0), ext_magnetic_field=(0.0, 0.0, 0.0), pauli_order_strategy=PauliOrderStrategy.ColorThenInteraction, coloring=None)

Generate a connectivity-aware qubit operator representing a quantum XYZ-type model.

This function implements the following Hamiltonian:

\[\hat{H} = \sum_{(j,k)\in E} (J_{x} \sigma_j^{x} \sigma_{k}^{x} + J_{y} \sigma_j^{y} \sigma_{k}^{y} + J_{z} \sigma_j^{z} \sigma_{k}^{z}) + \sum_{j\in V} (h_{x} \sigma_j^{x} + h_{y} \sigma_j^{y} + h_{z} \sigma_j^{z})\]

Where G(V,E) is the graph of the provided coupling map.

Note

There is often a \(-\frac{1}{2}\) factor included outside the summation of this equation. This factor is not applied internally, so it should be accounted for in the coupling_constants and ext_magnetic_field inputs.

>>> from qiskit.transpiler import CouplingMap
>>> from qiskit_addon_utils.problem_generators import generate_xyz_hamiltonian

>>> coupling_map = CouplingMap.from_line(10)
>>> hamiltonian = generate_xyz_hamiltonian(
...     coupling_map,
...     coupling_constants=(0.4, 0.4, 0.0),
...     ext_magnetic_field=(0.0, 0.0, 0.6),
... )
>>> print(hamiltonian)
SparsePauliOp(['IIIIIIIXXI', 'IIIIIIIYYI', 'IIIIIXXIII', 'IIIIIYYIII',
               'IIIXXIIIII', 'IIIYYIIIII', 'IXXIIIIIII', 'IYYIIIIIII',
               'IIIIIIIIXX', 'IIIIIIIIYY', 'IIIIIIXXII', 'IIIIIIYYII',
               'IIIIXXIIII', 'IIIIYYIIII', 'IIXXIIIIII', 'IIYYIIIIII',
               'XXIIIIIIII', 'YYIIIIIIII', 'IIIIIIIIIZ', 'IIIIIIIIZI',
               'IIIIIIIZII', 'IIIIIIZIII', 'IIIIIZIIII', 'IIIIZIIIII',
               'IIIZIIIIII', 'IIZIIIIIII', 'IZIIIIIIII', 'ZIIIIIIIII'],
            coeffs=[0.4+0.j, 0.4+0.j, 0.4+0.j, 0.4+0.j, 0.4+0.j, 0.4+0.j, 0.4+0.j, 0.4+0.j,
                    0.4+0.j, 0.4+0.j, 0.4+0.j, 0.4+0.j, 0.4+0.j, 0.4+0.j, 0.4+0.j, 0.4+0.j,
                    0.4+0.j, 0.4+0.j, 0.6+0.j, 0.6+0.j, 0.6+0.j, 0.6+0.j, 0.6+0.j, 0.6+0.j,
                    0.6+0.j, 0.6+0.j, 0.6+0.j, 0.6+0.j])

Parameters:

• coupling (CouplingMap | PyGraph | PyDiGraph) – The qubit subgraph on which to map the Hamiltonian. Directionality of graph edges will be ignored, and parallel edges will be treated as a single edge during generation of the operator.

• coupling_constants (Sequence[float]) – The real-valued coupling constants, \(J_i\), in each Cartesian axis.

• ext_magnetic_field (Sequence[float]) – The coefficients, \(h_i\), representing a magnetic field along each Cartesian axis.

• pauli_order_strategy (PauliOrderStrategy) – Indicates the iteration strategy in which the Pauli terms will be generated. See PauliOrderStrategy for more details.

• coloring (dict[tuple[int, int], int] | None) – An optional dictionary encoding the graph coloring that is used to sort the Hamiltonian terms. This dictionary maps edge labels (in the form of integer pairs) to color values (simple integers). Hamiltonian interaction terms will be added by increasing color value. Within each color, edges are sorted which does not change anything physically but results in easier to read results.

Returns:

A qubit operator describing a quantum XYZ-type model. The i-th qubit in the operator corresponds to the node in index i on the coupling map.

Raises:

• ValueError – The coupling constants must be specified by a length-3 sequence of floating point values.

• ValueError – The external magnetic field must be specified by a length-3 sequence of floating point values.

Return type:

SparsePauliOp

generate_time_evolution_circuit(operator, *, synthesis=None, time=1.0)

Model the time evolution of an operator.

>>> from qiskit.quantum_info import SparsePauliOp
>>> from qiskit.synthesis import SuzukiTrotter
>>> from qiskit.transpiler import CouplingMap
>>> from qiskit_addon_utils.problem_generators import (
...     PauliOrderStrategy,
...     generate_xyz_hamiltonian,
...     generate_time_evolution_circuit,
... )

>>> coupling_map = CouplingMap.from_line(6)
>>> hamiltonian = generate_xyz_hamiltonian(
...     coupling_map,
...     coupling_constants=(0.4, 0.4, 0.0),
...     ext_magnetic_field=(0.0, 0.0, 0.6),
...     pauli_order_strategy=PauliOrderStrategy.InteractionThenColorZigZag,
... )

>>> circ = generate_time_evolution_circuit(
...     hamiltonian, synthesis=SuzukiTrotter(order=2, reps=2), time=2.0
... )
>>> _ = circ.draw("mpl", fold=-1)

(png, hires.png, pdf)

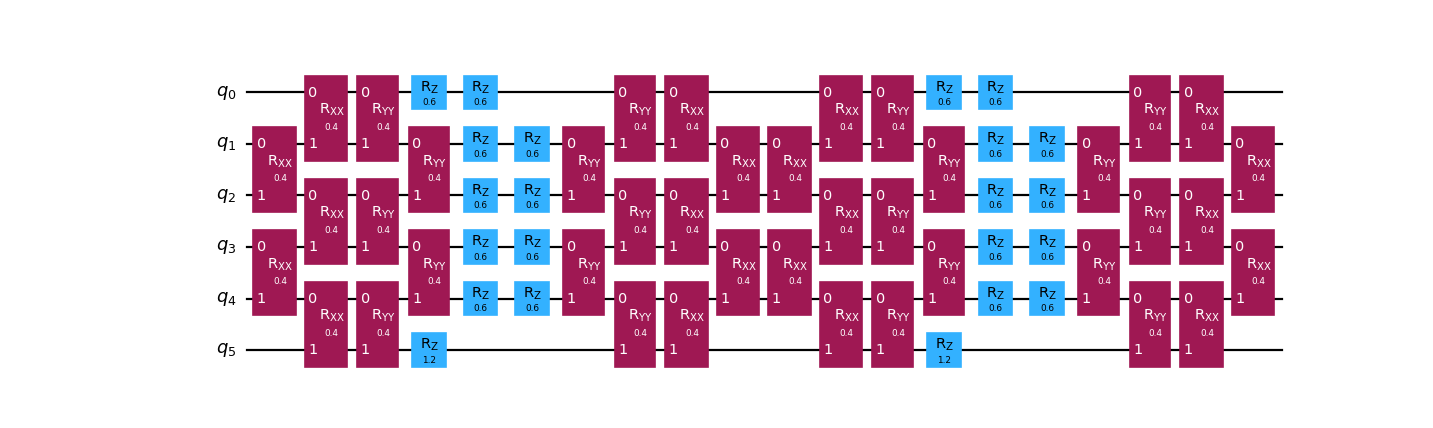
Parameters:

• operator (SparsePauliOp) – The operator for which to model the time evolution.

• synthesis (EvolutionSynthesis | None) – A synthesis strategy. If None, the default synthesis is the Lie-Trotter product formula with a single repetition.

• time (float) – The evolution time.

Returns:

A QuantumCircuit implementing a time-evolved operator.

Return type:

QuantumCircuit

class PauliOrderStrategy(value)

Enumeration of different Pauli-orderings.

When constructing a Hamiltonian on a colored set of edges, the generated Pauli terms can be ordered in different ways. This order of terms in the Hamiltonian is preserved during its time evolution and, thus, directly impacts the resulting quantum circuit.

ColorThenInteraction = 1

This strategy first iterates all edges (sorted by their color value) and then the interactions (sorted as X, Y, Z).

InteractionThenColor = 2

This strategy is the inverse to ColorThenInteraction. It first iterates the interactions (sorted as X, Y, Z) and then all edges (sorted by their color value).

InteractionThenColorZigZag = 3

This strategy is similar to the InteractionThenColor one. However, it alternates between iterating the edges by incrementing and decrementing color values as it jumps from one interaction to the next. For example, if only X and Y interactions are included and three color values are used ({1, 2, 3}), this will result in the following order: ["X on 1", "X on 2", "X on 3", "Y on 3", "Y on 2", "Y on 1"].