Using M3 with transpiled circuits

In the Basic usage section we looked at circuits with a qubit layout that was known ahead of time. However, when taking an arbitrary circuit and compiling it down to hardware, SWAP mapping permutes qubits such that the final mapping between virtual circuit qubits and physical qubits is not a-priori known. For example consider the Bernstein-Vazirani circuit

from qiskit import *
from qiskit_ibm_runtime.fake_provider import FakeCasablancaV2
import mthree

qc = QuantumCircuit(5, 4)
qc.reset(range(5))
qc.x(4)
qc.h(range(5))
qc.cx(range(4), 4)
qc.draw()
qc.h(range(4))
qc.barrier()
qc.measure(range(4), range(4))
qc.draw('mpl')

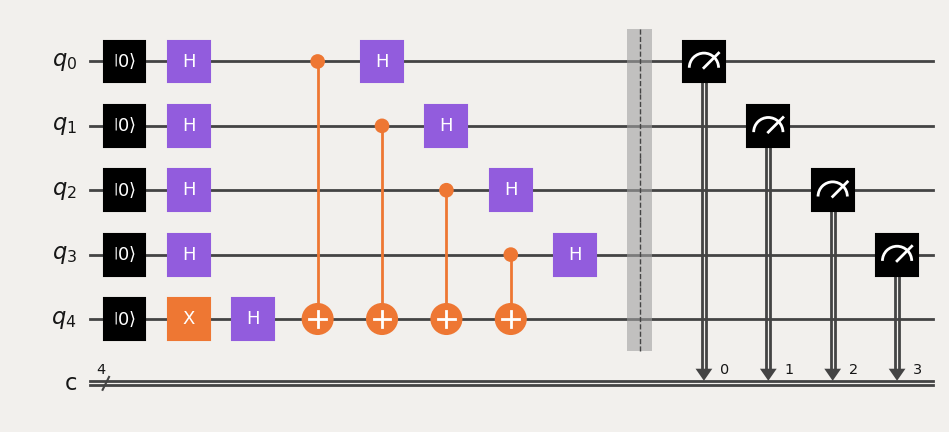
The target Casablanca system does not have the needed connectivity to natively embed the circuit and we must SWAP map it:

backend = FakeCasablancaV2()
trans_qc = transpile(qc, backend, optimization_level=3, seed_transpiler=12345)
trans_qc.draw('mpl')

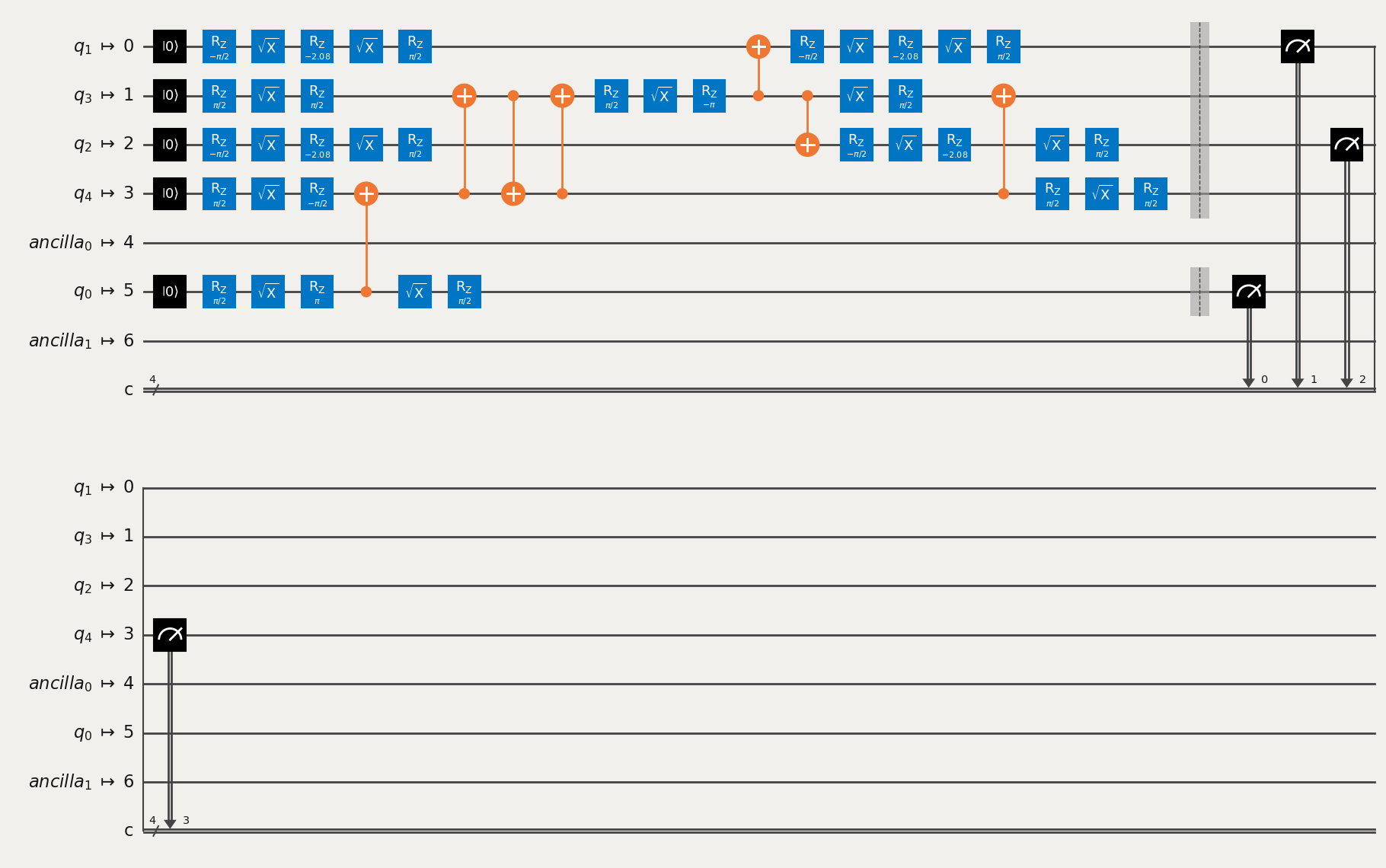
We can see from the measurements at the end that what was circuit qubit 0 is now mapped to physical qubit 5, circuit qubit 1 is mapped to physical qubit 3, etc… This information is needed to correctly mitigate the final results, yet outside of visually inspecting the circuit there is no easy way to obtain this information in Qiskit. As such, M3 includes the mthree.utils.final_measurement_mapping() routine to compute this for you:

mapping = mthree.utils.final_measurement_mapping(trans_qc)
print(mapping)

{0: 5, 1: 0, 2: 2, 3: 3}

We see that the keys of the returned dictionary label the classical bits used, and the corresponding values show which qubit was measured into that bit. Using this mapping in M3 is easy:

mit = mthree.M3Mitigation(backend)
mit.cals_from_system(mapping)

[<qiskit_aer.jobs.aerjob.AerJob at 0x7f654224dc30>]