Error analysis¶

Mitigating readout errors does not come for free. Instead, there is an overhaed that results in increased uncertainty in the computed results. M3 will optionally compute this overhead and return an upper-bound on the expected standard deviation (variance) of the computed expectation values.

Let us first calibrate the mitigator and get raw results:

from qiskit import *
from qiskit_ibm_runtime.fake_provider import FakeCasablancaV2
import mthree

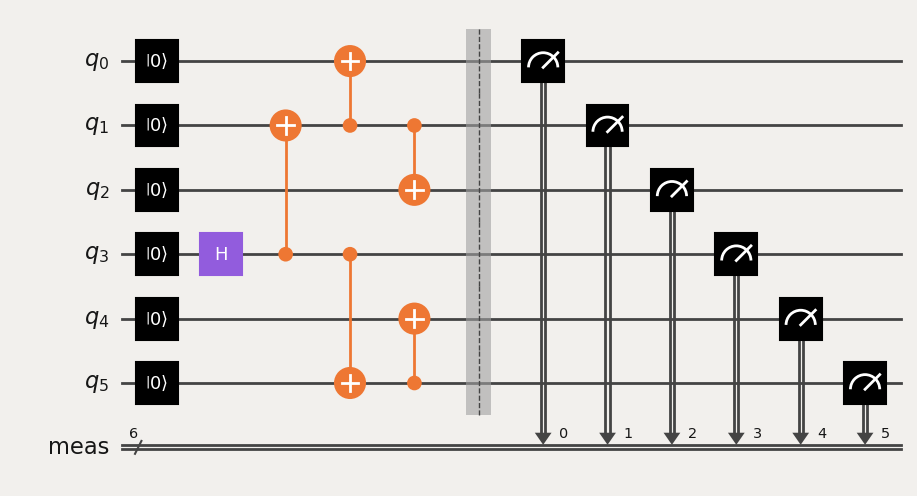
qc = QuantumCircuit(6)
qc.reset(range(6))
qc.h(3)
qc.cx(3,1)
qc.cx(3,5)
qc.cx(1,0)
qc.cx(5,4)
qc.cx(1,2)
qc.measure_all()
qc.draw('mpl')
_images/error_0_0.png 
backend = FakeCasablancaV2()
mit = mthree.M3Mitigation(backend)
mit.cals_from_system(range(6))

[<qiskit_aer.jobs.aerjob.AerJob at 0x7f34bc203c40>]

trans_qc = transpile(qc, backend)
raw_counts = backend.run(trans_qc, shots=8192).result().get_counts()

In order to compute the standard deviation of out mitigated expectation values we need to request the information be computed:

quasis = mit.apply_correction(raw_counts, range(6), return_mitigation_overhead=True)

The mitigation overhead is returned as an attribute of the returned quasi-probabilites

quasis.mitigation_overhead

np.float64(1.8092624565208555)

that, together with the number of shots taken, determines the upper-bound on the standard deviation:

quasis.stddev()

0.014861266213281373

It is also possible to return both the expectation value and standard deviation in a single call:

quasis.expval_and_stddev()

(0.9286051392555237, 0.014861266213281373)

Although this standard deviation is an upper-bound, it is usually a tight upper-bound that can be faithfully used futher analysis.