Grouped operators¶

Often times when evaluating expectation values it is possible to group operators together if the Pauli operators from which they are comprised commute with each other. when possible, this batching can greatly reduce the number of executions needed. To see how to do this consider the following simple example:

from qiskit import *
from qiskit_ibm_runtime.fake_provider import FakeAthensV2
import mthree

qc = QuantumCircuit(4)
qc.h(0)
qc.cx(0, range(1, 4))
qc.measure_all()
qc.draw('mpl')
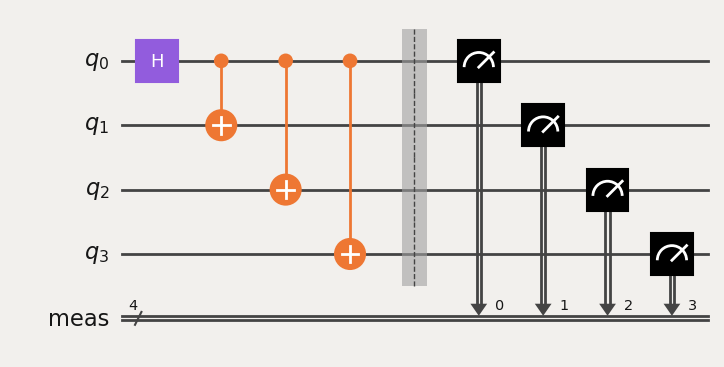
_images/grouped_0_0.png

Here we will generate and execute two circuits on the target system (fake system in this case), and, because we have transpiled, find the final measurement mapping:

backend = FakeAthensV2()
trans_circs = transpile([qc]*2, backend, optimization_level=3, approximation_degree=0)
mappings = mthree.utils.final_measurement_mapping(trans_circs)

Let us execute and get the resultant counts:

job = backend.run(trans_circs, shots=10000)
counts = job.result().get_counts()

We can now mitigate as usual:

mit = mthree.M3Mitigation(backend)
mit.cals_from_system(mappings, shots=10000)
quasis = mit.apply_correction(counts, mappings, return_mitigation_overhead=True)

Now that we have the final mitigated quasi-distributions we can compute expectation values. For batched operators, the expectation values are grouped together based on which quasi-distribution you want to evaluate them with:

quasis.expval([['IIII', 'ZZZZ', '0000', '1111'], ['IIII']])

[array([1.        , 0.9236816 , 0.49624482, 0.45133904], dtype=float32),
 array([1.], dtype=float32)]

The return list has the expectation values grouped into NumPy arrays. A similar procedure works for expectation values and standard deviations:

quasis.expval_and_stddev([['IIII', 'ZZZZ', '0000', '1111'], ['IIII']])

[(array([1.        , 0.9236816 , 0.49624482, 0.45133904], dtype=float32),
  0.012076842845159034),
 (array([1.], dtype=float32), 0.012076842879654787)]

If you have a single expectation value string then you do not need to wrap it in a list:

quasis.expval([['IIII', 'ZZZZ', '0000', '1111'], 'IIII'])

[array([1.        , 0.9236816 , 0.49624482, 0.45133904], dtype=float32), 1.0]

Of course probability-distributions work the same way as quasi-distributions:

probs = quasis.nearest_probability_distribution()
probs.expval([['IIII', 'ZZZZ', '0000', '1111'], ['IIII']])

[array([0.9999999 , 0.922718  , 0.49614546, 0.45123968], dtype=float32),
 array([1.], dtype=float32)]

probs.expval_and_stddev([['IIII', 'ZZZZ', '0000', '1111'], ['IIII']])

[(array([0.9999999 , 0.922718  , 0.49614546, 0.45123968], dtype=float32),
  0.012076842845159034),
 (array([1.], dtype=float32), 0.012076842879654787)]