Qiskit add-on: Propagated noise absorption (PNA)¶
PNA is a technique for mitigating errors in observable expectation values by “absorbing” the inverses of the learned noise channels into the observable using Pauli propagation. Each Pauli noise generator in the noise model is classically propagated to the end of the circuit and applied to the observable, resulting in a new observable that when measured on a QPU, mitigates the learned gate noise. Check out the tutorial to see how it works!
Overview¶
Executing entangling gates on modern QPUs results in a substantial amount of noise. Until fully fault tolerant devices are available, ideal entangling gates, \(U\), will not be available. They will instead be affected by some noise channel, \(\Lambda\).
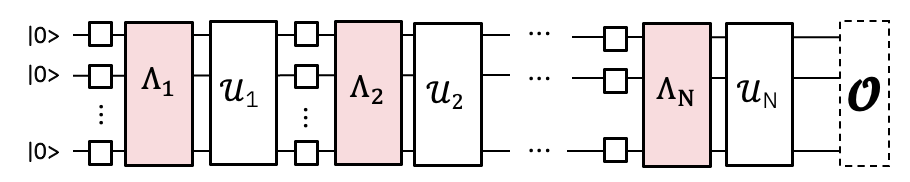
It is possible to learn and efficiently characterize this gate noise as a Pauli-Lindblad model, and as shown in probabilistic error cancellation (PEC), we can mitigate the error by implementing the anti-noise, \(\Lambda^{-1}\), with a QPU sampling protocol [1]. Other techniques, such as tensor-network error mitigation (TEM), implement the inverse noise channel as a classical post-processing step [2].

Like TEM, PNA implements the inverse noise channel in a classical processing step. While TEM uses tensor networks to describe and apply the noise-mitigating map to a set of informationally complete measurements, PNA uses Pauli propagation to propagate the observable, \(O\), through the inverse noise channel. This results in a new observable, \(\tilde{O}\), that when measured against the noisy state, mitigates the learned noise.

Sources of bias¶
This implementation propagates each Pauli error generator within each anti-noise channel, \(\Lambda^{-1}_i\), to the end of the circuit. As each anti-noise generator is propagated forward through the circuit under the action of \(N\) Pauli rotation gates of an \(M\)-qubit circuit, the number of terms will grow as \(O(2^N)\) towards a maximum of \(4^M\) unique Pauli components. To control the computational cost, terms with small coefficients must be truncated, which results in some error in the evolved anti-noise channel.
In addition to the truncation of the evolved anti-noise channel, \(\Lambda^{-1}\), \(\tilde{O}\) is also truncated as it is propagated through \(\Lambda^{-1}\). This is also a source of bias in the final mitigated expectation value.
While letting \(\tilde{O}\) grow larger during propagation will increase its accuracy, measuring it requires taking many more shots on the QPU. Typically this increases the coefficients of the original Pauli terms in \(O\), along with creating many new Pauli terms with smaller coefficients. Both the rescaling of the original coefficients and the creation of new terms can increase sampling overhead. In practice, we truncate once more by measuring only the largest terms in \(\tilde{O}\).
Installation¶
We encourage installing this package via pip, when possible:
pip install 'qiskit-addon-pna'
For more installation information refer to the installation instructions in the documentation.
Citing this project¶
If you use this package in your research, please cite it according to CITATON.bib file included in this repository:
@software{qiskit-addon-pna,
author = {Qiskit addons team},
title = {{Qiskit addon: Propagated noise absorption}},
howpublished = {\url{https://github.com/Qiskit/qiskit-addon-pna}},
year = {2025}
}
Deprecation Policy¶
We follow semantic versioning and are guided by the principles in Qiskit’s deprecation policy. We may occasionally make breaking changes in order to improve the user experience. When possible, we will keep old interfaces and mark them as deprecated, as long as they can co-exist with the new ones. Each substantial improvement, breaking change, or deprecation will be documented in the release notes.
Contributing¶
The source code is available on GitHub.
The developer guide is located at CONTRIBUTING.md in the root of this project’s repository. By participating, you are expected to uphold Qiskit’s code of conduct.
We use GitHub issues for tracking requests and bugs.
License¶
References¶
[1] Ewout van den Berg, et al., Probabilistic error cancellation with sparse Pauli-Lindblad models on noisy quantum processors, arXiv:2201.09866 [quant-ph].
[2] Sergei Filippov, et al., Scalable tensor-network error mitigation for near-term quantum computing, arXiv:2307.11740 [quant-ph].