Sample-based quantum diagonalization (SQD) overview

Sample-based quantum diagonalization (SQD) is a classical post-processing technique which acts on samples obtained from a quantum circuit after execution on a QPU. It is useful for finding eigenvalues and eigenvectors of quantum operators, such as the Hamiltonian of a quantum system, and uses quantum and distributed classical computing together. This post-processing technique may be especially useful for users simulating chemical or other quantum systems.

Classical computing is used to process samples obtained from a quantum processor, and to project and diagonalize a target Hamiltonian in a subspace spanned by them. This allows SQD to be robust to samples corrupted by quantum noise and manage large Hamiltonians, such as chemical systems with millions of interacting terms, beyond the reach of exact diagonalization methods.

The SQD tool can target Hamiltonians expressed as linear combinations of Pauli operators or second-quantized Fermionic operators. The input samples are obtained by quantum circuits defined by the user, which are believed to be good representations of eigenstates (for example, the ground state) of a target operator. The convergence rate of SQD as a function of the number of samples improves with the sparseness of the target eigenstate.

Install the SQD package

There are two ways to install the SQD package: PyPI and building from source. It is recommended to install these packages in a virtual environment to ensure separation between package dependencies.

Install from PyPI

The most straightforward way to install the qiskit-addon-sqd package is via PyPI.

pip install qiskit-addon-sqd

Build from source

git clone git@github.com:Qiskit/qiskit-addon-sqd.git

pip install tox notebook -e '.[notebook-dependencies, dev]'

Theoretical background

The SQD workflow using self-consistent configuration recovery is explained in detail in [1]. This section provides an overview to the technique depicted in the following diagram.

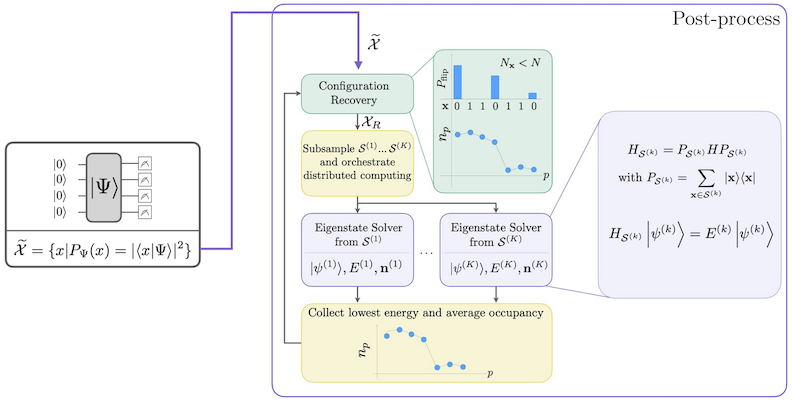
Here $\bar{\mathcal{X}}$ is a set of noisy samples which contain, in the context of the Hamiltonian being simulated, physical and non-physical configurations (represented as bitstrings) obtained from execution on a QPU. The non-physical configurations are due to noise and can be processed by the sqd.configuration_recovery.recover_configurations() method to refine the samples into a new set $\mathcal{X}_R$.

From this set, batches of configurations $\mathcal{S}^{(1)}...\ \mathcal{S}^{(K)}$ are collected according to a distribution proportional to the empirical frequencies of each $\mathbf{x}$ in $\mathcal{X}_R$. Each batch of sampled configurations spans a subspace, $\mathcal{S}^{(k)}: k = 1, ..., K$, in which the Hamiltonian is projected and diagonalized:

$\hat{H}_{S^{(k)}} = \hat{P}_{\mathcal{S}^{(k)}}\hat{H}\hat{P}_{\mathcal{S}^{(k)}}\text{, with } \hat{P}_{\mathcal{S}^{(k)}} = \sum_{\mathbf{x} \in \mathcal{S}^{(k)}} |\mathbf{x}\rangle\langle\mathbf{x}|,$

where $\hat{H}_{\mathcal{S}^{(k)}}$ is the Hamiltonian of a given subspace.

The bulk of the SQD workflow lies here wherein each of these subspace Hamiltonians is diagonalized. The ground states obtained from each of these subspaces, $|\psi^{(k)}\rangle$, are used to obtain an estimate of a reference vector of occupancies $\mathbf{n}^{(K)}$ averaged over each of the $K$ subspaces. A new set of configurations $\mathcal{X}_R$ is then generated by probabilistically flipping individual bits based on this average occupation and the known total number of particles (hamming weight) in the system. This configuration recovery process is then repeated by preparing a new set of subspaces to diagonalize, obtaining new eigenstates and averaged orbital occupancy, then generating a new set of configurations. This loop is iterated until a user specified criterion is met, and the overall process is analogous to filtering a noisy signal to improve its fidelity.

Next steps

References

[1] Robledo-Moreno, Javier, et al. "Chemistry beyond exact solutions on a quantum-centric supercomputer" arXiv preprint arXiv:2405.05068 (2024).