Approximate quantum compiler with tensor networks (AQC-Tensor)

The Approximate quantum compilation with tensor networks (AQC-Tensor) Qiskit addon enables users to compile the initial portion of a circuit into a nearly equivalent approximation of that circuit, but with much fewer layers. This is accomplished using tensor networks using the method described in [1]. Its primary utility is in circuits which simulate time evolution, but may be applicable to any class of circuits which has access to:

1. A great intermediate state, known as the “target state,” that can be achieved by tensor-network simulation; and,
2. A good circuit that prepares an approximation to the target state, but with fewer layers when compiled to the target hardware device.

The technique generates an ansatz circuit based on a larger target circuit which a user ultimately wants to execute on a QPU. This is accomplished by first simulating some portion of the target circuit by tensor network methods and obtaining an accurate description of an intermediate state which the ansatz circuit will approximate. Once this intermediate state is found, it is used as a cost function in order to optimize the ansatz circuit's parameters. After the optimization is complete, the remaining portion of the target circuit is appended to the ansatz and then executed on quantum hardware.

Install the AQC-Tensor package

There are two ways to install the AQC-Tensor package: PyPI and building from source. It is recommended to install these packages in a virtual environment to ensure separation between package dependencies.

Install from PyPI

The most straightforward way to install the AQC-Tensor package is via PyPI. In order to use the package, you must also install at least one tensor network backend. The following code snippet will install the addon, along with quimb (for tensor network support) and jax (for automatic differentiation). If you are interested, check out the package on GitHub

pip install 'qiskit-addon-aqc-tensor[quimb-jax]'

Install from source

git clone git clone git@github.com:Qiskit/qiskit-addon-aqc-tensor.git

pip install tox jupyterlab -e '.[notebook-dependencies,dev]'

Theoretical Background

The AQC-Tensor procedure is explained in detail in [1]. This section provides an overview of the technique.

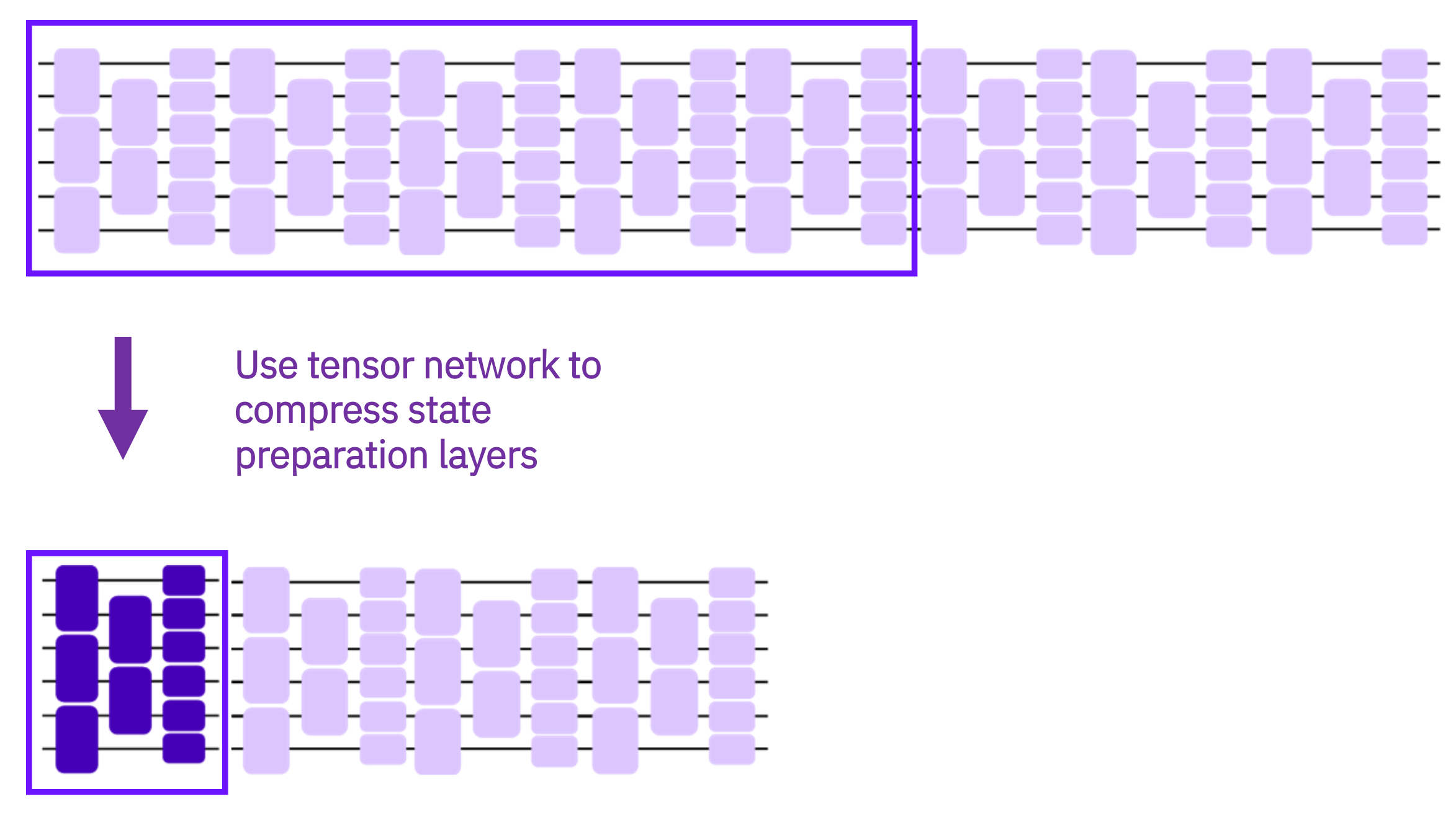
In general, AQC-Tensor requires three things as input:

1. A description of the target state in the form of a tensor network. This can be generated by simulating a circuit on a tensor network simulator, or it could be generated in some other way (for example, by performing time evolution on a matrix-product state using the time-dependent variational principle).
2. A parametrized ansatz circuit. Ideally one which contains hardware-efficient connectivity, such that it will have a reasonable depth on the target hardware.
3. Initial parameters to plug into the ansatz circuit, such that the resulting state is already a good approximation of the target state. (This is not, in principle, required for AQC, but it helps to give the optimizer a sensible starting point.)

The technique is to then iteratively optimize the parameters of the ansatz circuit, such that the state it generates is as close to the target state as possible.

Ansatz generation

To generate (2) and (3) from the above list, the qiskit-addon-aqc package possesses a function, generated_ansatz_from_circuit() which will take an input circuit and outputs a parameterized ansatz and initial set of parameters. The parameters returned by the function are such that, when plugged into the ansatz, will generate a state that is exactly equivalent to the input circuit, up to a global phase.

The ansatz which is generated by this function uses 9 parameters per two-qubit block and is based on the KAK decomposition, which parametrizes any two-qubit gate in terms of three parameters, up to single-qubit rotations. The single-qubit rotations are then decomposed as $ZXZ$, each of which has three parameters. This results in the ansatz circuit containing 3 parameters for each two-qubit block of the original circuit, plus 3 parameters for an outgoing single-qubit rotation on each of the two qubits (for a total of 9 parameters). After adding these blocks, the ansatz is completed by adding a layer of single-qubit rotations to each active qubit at the start of the circuit.

Tensor-network simulation

To obtain a description of the target state which is desired, this addon uses a matrix product state (the simplest form of a tensor network) and supports the following tensor-network simulators:

• MPS simulator found in Qiskit Aer
• Quimb's eager CircuitMPS simulator
• Quimb's lazy Circuit simulator

The most important parameter of a tensor network is its maximum bond dimension, $\chi$. This parameter limits how much entanglement can be represented with a tensor network, and thus to what depth a given circuit can be faithfully simulated.

Given a circuit with $L$ qubits, a matrix-product state needs at most a bond dimension of $\chi_{exact} = 2^{L/2}$ in order to exactly simulate the circuit to any depth. This is out of reach for general utility-scale circuits acting on 100+ qubits. For this reason, if you are attempting to experiment with this addon for a toy-problem with few qubits, it is important to ensure that $\chi < 2^{L/2}$. This way, when you scale the problem to a larger circuit, the target state remains classically simulable.

Next steps

References

[1] Robertson, Niall F., et al. "Approximate Quantum Compiling for Quantum Simulation: A Tensor Network based approach" arXiv preprint arXiv:2301.08609 (2023).